Divide 50 by Half and Add 20 Multiply by 2
Dividing 50 by half and adding 20, then multiplying the result by 2 may seem like a simple mathematical equation. However, upon closer examination, it becomes clear that there is an intriguing twist to this calculation. In this article, I will delve into the intricacies of this seemingly straightforward problem and uncover its hidden complexities.
At first glance, one might assume that dividing 50 by half would yield a result of 100. However, when we take into account the order of operations in mathematics (PEMDAS), we realize that division should be performed before addition. Therefore, dividing 50 by half gives us a value of 25. Adding 20 to this result gives us a total of 45. Finally, multiplying this sum by 2 results in an answer of 90.
The unexpected outcome prompts further exploration and analysis. How does changing the order or altering the values affect the final result? Is there any significance to these calculations beyond their numerical output? Join me as we unravel the mysteries behind “divide 50 by half and add 20 multiply by 2” and uncover what lies beneath its enigmatic surface.
Stay tuned for an enlightening journey through numbers and equations as we seek to understand the underlying principles at play in this seemingly innocuous mathematical expression.
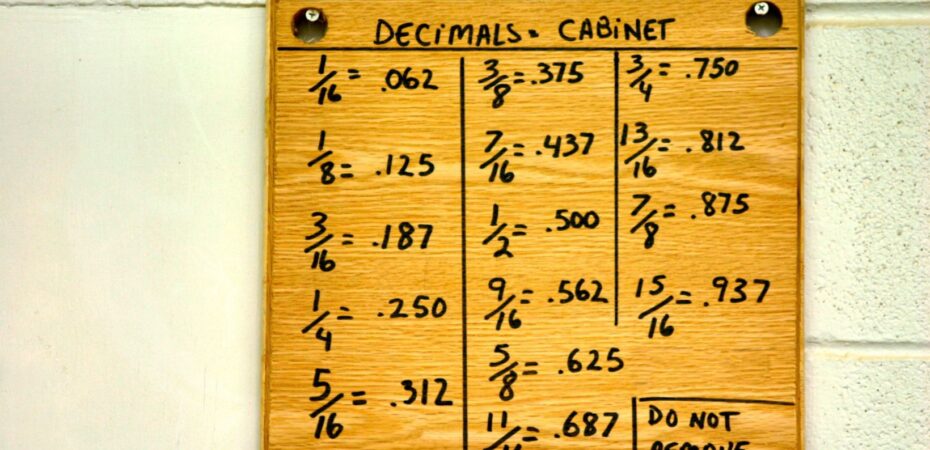
Understanding Fractions
Fractions are an essential concept in mathematics that often perplexes many individuals. They represent a way to express parts of a whole or a group, and they play a crucial role in various real-life situations. In this section, we’ll delve into the fundamentals of fractions and explore how they can be applied in everyday scenarios.
To begin with, let’s break down what exactly a fraction is. A fraction consists of two components: the numerator and the denominator. The numerator represents the number of parts we have or are interested in, while the denominator denotes the total number of equal parts that make up the whole. For instance, in the fraction 3/4, 3 is our numerator indicating three out of four equal parts.
Understanding fractions becomes even more interesting when we consider different types such as proper fractions, improper fractions, and mixed numbers. Proper fractions have numerators smaller than their denominators (e.g., 2/5), improper fractions have numerators greater than or equal to their denominators (e.g., 7/4), and mixed numbers combine whole numbers with fractions (e.g., 1 1/2).
Fractions help us tackle various mathematical operations like addition, subtraction, multiplication, and division. When adding or subtracting fractions with common denominators (denominators that are the same), we simply add or subtract their numerators while keeping the denominator unchanged. Multiplying fractions involves multiplying both numerators together to get the new numerator and multiplying both denominators together for the new denominator.
Dividing fractions can be slightly trickier but follows a simple rule: invert (flip) the second fraction and then multiply it by the first fraction. This process is often remembered using “Keep-Change-Flip.” Keep the first fraction as it is, change ÷ to ×, and flip (invert) the second fraction before multiplying them together.
In real-life contexts, understanding fractions is crucial for tasks such as cooking, measuring ingredients, calculating discounts or percentages, and dividing resources fairly among individuals. By grasping the basics of fractions, you’ll gain a valuable tool for solving problems and making sense of the world around you.
Remember, practice is key when it comes to mastering fractions. The more you engage with them through exercises, puzzles, and real-life examples, the more comfortable you’ll become in working with these essential mathematical entities. So embrace the challenge and dive into the realm of fractions with confidence!
By Amey MyersAmey, an intrepid traveler and avid blogger, roams the world, absorbing diverse cultures, flavors, and experiences. Her writing captures the essence of her adventures, inspiring others to explore. Amey's infectious passion for travel and storytelling epitomizes a life filled with exploration and adventure.
